Poker Bankroll Risk Of Ruin Calculator

The bankroll required to have a one percent risk of ruin is about 20 percent higher than the bankroll for a five percent risk of ruin. The bankroll as a percentage of the total dollars played decreases as the number of plays increases. SINGLE VERSUS MULTIPLE PLAY WITH SAME BET AMOUNT. Nov 18, 2013 Risk of Ruin Simulator and Calculator I built a function that works in a free program (called R - you can download it at www.r-project.org ) for simulating your risk of ruin. I have pasted the function below, but first let me explain a few things.

Risk of ruin is a concept in gambling, insurance, and finance relating to the likelihood of losing all one's investment capital^[1] or extinguishing one's bankroll below the minimum for further play. For instance, if someone bets all their money on a simple coin toss, the risk of ruin is 50%. In a multiple-bet scenario, risk of ruin accumulates with the number of bets: each repeated play increases the risk, and persistent play ultimately yields the stochastic certainty of gambler's ruin.

• 1Finance

Live Poker Bankroll Management

Risk Of Ruin Calculator Blackjack

Finance[edit]

The bankroll required for a one percent risk of ruin is about 24 percent higher than the bankroll required for a five percent risk of ruin. The bankroll as a percent of the total dollars played, decreases as the number of plays increases. MULTIPLE PLAY DOUBLE BONUS POKER.

Risk of ruin for investors[edit]

• Going broke and having no money to play with is any poker players worst nightmare; thus is it worthwhile getting used to using this calculator to understand and negate the risk. To take our first example of 3bb/100 winrate with a standard deviation of 100 bb/100 we will get approximately a 5,000 bb bankroll or 50BI for a risk of ruin of 5%.
• Increased Risk Of Ruin Most would agree that the above bankroll building strategy is aggressive, only requiring 20 or 25 buy-ins to take a shot at the next level. Anything more ambitious would invite a risk of ruin that is difficult to overcome.

Two leading strategies for minimising the risk of ruin are diversification and hedging. An investor who pursues diversification will try to own a broad range of assets – they might own a mix of shares, bonds, real estate and liquid assets like cash and gold. The portfolios of bonds and shares might themselves be split over different markets – for example a highly diverse investor might like to own shares on the LSE, the NYSE and various other bourses. So even if there is a major crash affecting the shares on any one exchange, only a part of the investors holdings should suffer losses. Protecting from risk of ruin by diversification became more challenging after the financial crisis of 2007–2010 – at various periods during the crises, until it was stabilised in mid-2009, there were periods when asset classes correlated in all global regions. For example, there were times when stocks and bonds ^[2] fell at once – normally when stocks fall in value, bonds will rise, and vice versa. Other strategies for minimising risk of ruin include carefully controlling the use of leverage and exposure to assets that have unlimited loss when things go wrong (e.g., Some financial products that involve short selling can deliver high returns, but if the market goes against the trade, the investor can lose significantly more than the price they paid to buy the product.)

The probability of ruin is approximately

${\displaystyle P(\mathrm{r}\mathrm{u}\mathrm{i}\mathrm{n})={\left(\frac{2}{1+\frac{\mu }{r}}-1\right)}^{\frac{s}{r}}}$,

where

Northern california casinos with roulette tables. River Rock Roulette is the newest sensation to hit Sonoma County and it's exclusive to River Rock Casino! The layout and payouts are the same as traditional roulette, only the cards represent the winning number instead of a ball. Get into the action by picking a single lucky number, splits, or small combinations of your favorite numbers.

${\displaystyle r=\sqrt{{\mu }^2+{\sigma }^2}}$

for a random walk with a starting value of s, and at every iterative step, is moved by a normal distribution having mean μ and standard deviation σ and failure occurs if it reaches 0 or a negative value. For example, with a starting value of 10, at each iteration, a Gaussian random variable having mean 0.1 and standard deviation 1 is added to the value from the previous iteration. In this formula, s is 10, σ is 1, μ is 0.1, and so r is the square root of 1.01, or about 1.005. The mean of the distribution added to the previous value every time is positive, but not nearly as large as the standard deviation, so there is a risk of it falling to negative values before taking off indefinitely toward positive infinity. This formula predicts a probability of failure using these parameters of about 0.1371, or a 13.71% risk of ruin. This approximation becomes more accurate when the number of steps typically expected for ruin to occur, if it occurs, becomes larger; it is not very accurate if the very first step could make or break it. This is because it is an exact solution if the random variable added at each step is not a Gaussian random variable but rather a binomial random variable with parameter n=2. However, repeatedly adding a random variable that is not distributed by a Gaussian distribution into a running sum in this way asymptotically becomes indistinguishable from adding Gaussian distributed random variables, by the law of large numbers.

Risk Of Ruin Calculator Poker

Financial trading[edit]

The term 'risk of ruin' is sometimes used in a narrow technical sense by financial traders to refer to the risk of losses reducing a trading account below minimum requirements to make further trades. Random walk assumptions permit precise calculation of the risk of ruin for a given number of trades. For example, assume one has $1000 available in an account that one can afford to draw down before the broker will start issuing margin calls. Also, assume each trade can either win or lose, with a 50% chance of a loss, capped at $200. Then for four trades or less, the risk of ruin is zero. For five trades, the risk of ruin is about 3% since all five trades would have to fail for the account to be ruined. For additional trades, the accumulated risk of ruin slowly increases. Calculations of risk become much more complex under a realistic variety of conditions. To see a set of formulae to cover simple related scenarios, see Gambler's ruin. Opinions among traders about the importance of the 'risk of ruin' calculations are mixed; some^[who?] advise that for practical purposes it is a close to worthless statistic, while others^[who?] say it is of the utmost importance for an active trader to be aware of it.^[3][4]

See also[edit]

Poker Risk Of Ruin Calculator

• Absorbing Markov chain (used in mathematical finance to calculate risk of ruin)
• Fat-tailed distribution (exhibits the difficulty and unreliability of calculating risk of ruin)
• St. Petersburg paradox (an imaginary game with no risk of ruin and positive expected returns, yet paradoxically perceived to be of low investment value)

Notes and references[edit]

1. ^'Risk of Ruin (Forex Glossary)'. Financial Trading Journal. Retrieved April 26, 2012.
2. ^Though US treasuries were generally an exception, except on the very worst days their value generally rose, as part of the 'Flight to safety'.
3. ^Trading Risk: Enhanced Profitability through Risk Control Kenneth L Grant (2009)
4. ^The trading game Ryan Jones (1999)

Further reading[edit]

Video Poker Risk Of Ruin Calculator

• Dickson, David C. M. (2005). Insurance Risk And Ruin. Cambridge University Press. Retrieved April 26, 2012.ISBN0521846404
• Powers, Mark J. (2001). Starting Out in Futures Trading. McGraw-Hill. pp. 52–55. Retrieved April 26, 2012.ISBN0071363904
• Baird, Allen Jan (2001). Electronic Trading Masters: Secrets from the Pros!. John Wiley & Sons, Inc. pp. 30–32. Retrieved April 26, 2012.ISBN0471401935

By John Grochowski
My friend Mark isn’t a casino regular, but he likes to play a little video poker now and then. His goal is just to have a good time and stay in action for a couple of hours.
“Do you have a guide to how much cash I need to last a couple of hours?” he asked.
I showed him the bankroll calculator on Video Poker for Winners software, and assumed expert play for 1,000 hands --- about two hours play for an average player.
First up was Jacks or Better on three pay tables --- the full-pay 9-6 game, paying 9-for-1 on full houses and 6-for-1 on flushes, which returns 99.54 percent with expert play; the 8-5 game (97.30 percent); and the 7-5 game (96.15 percent) that’s becoming all too common on quarter games.
Jacks or Better is the least volatile of common video poker games, a game that’s designed to keep you in your seat. There are no big four-of-a-kind bonuses that are going to make your day. All quads pay 125 coins for a five-coin wager. But the 2-for-1 payoff on two pairs packs a different kind of wallop, one that will keep you going for extra chances at the bigger pays.
The average loss for two hours of betting $1.25 a hand on a quarter machine is $5.75 with a 9-6 pay table, $34.75 at 8-5 and $48.12 at 7-5 --- which ought to tell you why I’m always harping on finding the best pay tables. In the days when each video poker machine had just one game --- no touching the screen to try a different game --- I once found a long row of 18 machines that alternated between 9-6 and 8-5 pay tables. There were as many players at the low-payers as at the 9-6ers. Ugh.
The required bankroll is much higher than the average loss if you want to give yourself enough for a 5 percent risk of ruin --- a 95 percent chance of surviving two hours without losing it all. That takes $165 on 9-6 Jacks, $185 at 8-5 and $195 at 7-5.
Your chances of having a winning session after two hours are 34.54 percent at 9-6, 22.35 percent at 8-5 and 17.19 percent at 7-5. Settling for a 7-5 pay table instead of 9-6 cuts your chances of winning in half.
Then I checked probably the most popular video poker game: Double Double Bonus Poker. With a 9-6 pay table, it’s a 98.98 percent return, $12.75 average loss in two hours on a quarter machine, with a $300 bankroll for a 5 percent risk of ruin and a 35.46 percent chance of a winning session. On the 8-5 version that’s become all too common, the payback percentage falls to 96.79 percent, average two-hour loss increases to $40.12, the bankroll requirement rises to $320, and the chance of a winning session drops to 30.75 percent.
Double Double Bonus Poker is the more volatile game, with more of its payback concentrated into relatively rare four-of-a-kind hands. Most quads pay 250 for a five-coin wager, and the reward rises to 400 on four 2s, 3s or 4s; 800 if those low quads are accompanied by an Ace, 2, 3 or 4 kicker; 800 on four Aces; and 2,000 on four Aces with a 2, 3 or 4 kicker. The two-pairs return is reduced to 1-for-1 ---- you just get your money back.
That’s why Double Double Bonus bankroll requirements are higher than in Jacks or Better. But in any game, cuts in the pay table slash your chances of winning. Be wary.
LONGER SESSIONS: Two-hour sessions are extremely volatile. Just about anything can happen in any session as short as a couple of hours. But I’ve had many a two-hour session back when that was the length of a riverboat casino cruise, and still often go to a local casino to play for a couple of hours and have lunch or dinner.
But what if you’re going to play longer? What if you’re going on an overnight stay and figure to get in, say, 10 hours of play? Do you have to multiply two-hour bankroll requirements by five?
No, you don’t. Longer sessions smooth things out a bit. For 10 hours of quarter play on 9-6 Jacks or Better, the bankroll for a 5 percent risk of ruin doesn’t quintuple from $165 to $825. Instead, it’s less than tripled, at $450, while the bankroll requirement for 8-5 Jacks rises to $570.
On the more volatile Double Double Bonus Poker, that $300 bankroll for a 5 percent risk or ruin for two hours rises to $885. That’s a big chunk of cash, but at least it’s not the $1,500 you get when multiplying the $300 by five. On the 8-5 version, the bankroll needed for 10 hours is $1,010, and that’s one reason I just won’t play 8-5 Double Double Bonus Poker.

Risk Of Ruin Calculator Video Poker

John Grochowski writes about casino games and the gambling industry in his weekly 'Gaming' column, which is syndicated in newspapers and Web sites across the United States. John is also the author of six books on casinos and casino games.

The amateur does not need to make money playing poker and so can afford to take shots more aggressively than can someone who depends on poker income. In this article, we want to discuss several important features of bankroll management for semi-professionals and professionals, including the purpose of the bankroll, the relationship between bankroll and the limits that one can play, taking shots at higher limits, dropping limits, growing your bankroll, and setting goals for your play and income.

Define the Goal Of Bankroll

Let’s begin with an examination of the purpose of your bankroll. What exactly is the point of having this thing and why does it matter? Essentially the bankroll allows you to “invest” in a particular level of play. The higher the level of play, the more income you can potentially make. Thus, the bankroll is what allows the professional to make money. Of course, you can sit with your entire bankroll in one game and have a high potential for profit, but you also have a high potential for losing it all and ending your career as a poker player.

The professional player must find the happy medium between maximum profit and minimal or at least acceptable risk. The bankroll, then, allows one to play almost indefinitely while maintaining a solid profit level. The bankroll is only a means to this real goal of earning income. The bankroll is not an end in itself and this fact must be kept in mind. Should your bankroll take a hit in the course of a bad week, this is not necessarily any reason to become upset or concerned. The bankroll is only a tool to be used in generating your income. Now, although it is only a means to the real end, it is a rather important tool and care must used in making decisions that impact it.

What exactly is the relationship between your bankroll and the level (or blind amounts) that you can play? As all poker players know, this game brings a certain amount of variance. Bad beats happen, and sometimes they can happen in rapid succession or for extended periods of times in big pots. This is the inherent risk of playing poker. Chance creates a risk of loss. You cannot do anything about the element of chance, but you can take steps to minimize its effect on your ability to earn an income playing poker. By having a bankroll large enough to absorb the downswings you can be relatively certain that you can play indefinitely and thus, indefinitely earn an income. A player with a $100K bankroll can almost certainly play a $1/$2 no limit hold’em game for as long as he/she would like. With a bankroll this large, however, the player could play at much higher levels, earning greater income while also being relatively certain of the ability to continue playing at that higher level indefinitely, but where exactly is that line?

This brings us to the more intricate question of how much bankroll one needs for a given blind level. There are several answers to this question, but we are going to limit my analysis to three or rather two and a half. The first is the conventional rule for big bets or buy-ins. In limit poker the conventional rule is 300 big bets (BBs). Thus, if you wanted to play a 5/10 limit game, you would need a bankroll of $3000. In a no limit game, the conventional rule is 20 buy-ins or 2000 big blinds (bbs). Thus, to play in a $2/$4 no limit game, you would need a bankroll of $8000.

Along these lines, Chris Ferguson has endorsed a 5% rule for no limit games. You should not have more than 5% of your bankroll on the table and if your stack reaches 10% of your bankroll then you should leave the table. This is quite similar to the conventional rule, since 5% of $8000 is $400, or one table buy-in. It could be used for limit poker also, but without a standard buy-in amount, it could be misused. For example, a player with a $100 bankroll might sit in a 1/2 game with $5. It is probably best to confine Ferguson’s strategy to no limit. Ferguson’s approach also reduces risk by limiting how much money you can have in front of you at a table, which is not something the conventional rule addresses.

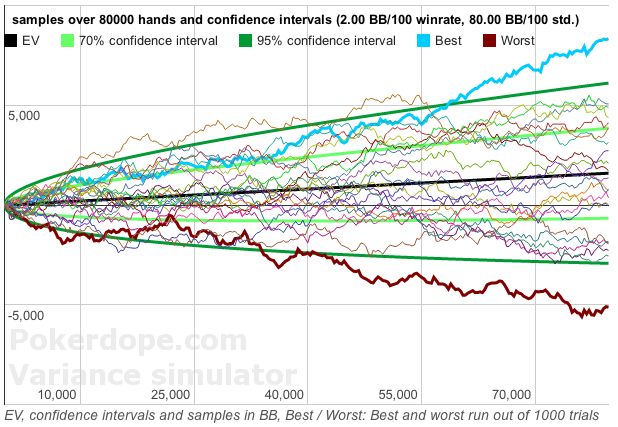
Bankroll Management Examples

A third strategy operates from a risk of ruin perspective. On this strategy one chooses an acceptable level of risk and determines the necessary bankroll given one’s playing style. While the first two strategies appear sound, this final approach is more precise and can be tailored to your own game rather than a blanket rule that will not be appropriate for many players. How does this work? You will need to know your win rate and your standard deviation. I’ll assume readers understand win rate, so I’ll only explain standard deviation. Standard deviation is a measure of the distribution of your wins and losses in each session around your win rate. Thus, if you play five sessions of an hour each, your win rate would be $16/hr and your standard deviation would be $68.95/hr given the following results:

Session 1 – won $30
Session 2 – lost $50
Session 3 – lost $100
Session 4 – won $75
Session 5 – won $125

How do we calculate the standard deviation? If you have a tracking program, it will probably do this for you, but if you do not have such a system you will need to calculate it yourself. Once you know how, it is relatively simple. You first need to standardize all session amounts into $/hr. In the example above we made this unnecessary by stipulating that each session was an hour in length. If, however, the first session were two hours in length, then you would refigure the amount as $15/hr for that session. Second, you determine the difference between each session result and your win rate. So, for example, you would subtract $16 from $30 for the first session to get $14, and so forth. You then square all of these numbers; i.e., $14 times $14 and so forth, and take the sum of each square. Finally, you will then average this sum.

So, in our example, you would divide 23,770 by 5 (number of sessions) to arrive at a variance of 4754. To determine the standard deviation you then take the square root of variance, which in this case is $68.95/hr. If you want to calculate your bankroll requirement, however, you only need the variance number. One final note: as a rule of thumb, you should have at least thirty sessions of data before you can expect a reasonably accurate standard deviation number. I’ve used only five to simplify the discussion.

Once we have these figures we can then determine our bankroll requirement. The bankroll formula is: -(SD*SD)/(WR*2)ln(risk of ruin). NOTE: standard deviation (SD) times itself (SD*SD) is simply variance. You can calculate for any risk of ruin you like, but if you are playing professionally you will want a minimum of 1% risk of ruin. With this number your chances of going bust are only 1 in 100. You could work with an even smaller risk of ruin, but this can get rather conservative. As a shorthand reference, the ln(1% risk of ruin) is -4.605 and for 0.1% it is -6.908. Now, if we continue with our example, a 1% risk of ruin requires a bankroll of: [(4754)/(16*2)](-4.605), which reduces to -[4754/32](-4.605), and this equals $3420.65. So, in our example the pro would need a bankroll of $684.13 to play in the current game with a 1% risk of ruin.

Now, that is the basic approach, but an important wrinkle must be borne in mind. If you were to withdraw all of your winnings, your risk of ruin would actually be 100%. Why is this? If you play indefinitely, never replenishing the bankroll, the natural variance of the game would gradually deplete the entire bankroll. It might take a long time for this to happen, but you can be reasonably certain that it would happen.

What Do Professionals Choose?

Professional players take a certain portion of their winnings for living expenses, but leave the remainder to grow the bankroll. The remainder is what we will refer to as the effective win rate. Thus, we will distinguish between the table win rate (i.e., what you make playing at the table) and the effective win rate (table win rate minus withdrawals for living expenses). For example, if a pro makes $20/hr playing at the table but withdraws $15/hr as her salary then her effective win rate is only $5/hr. This is rather important as the difference between the table win rate and the effective win rate generates vastly different bankroll requirements. Consider a pro who makes $20/hr at the table but whose effective win rate is only $5/hr and who also has a standard deviation of $100/hr. If we solve for a 1% risk of ruin with the table win rate, we get a bankroll requirement of $1151.25. If we solve for the effective rate, however, we get a bankroll requirement of $4605. Now that’s quite a difference!

This difference underscores the advantage of this third bankroll strategy over the two previous strategies. Neither the conventional rule nor Ferguson’s strategy accounts for the difference between a table win rate and the effective win rate. Moreover, neither strategy is equipped to take account of differing table win rates and standard deviation for varying players. Ferguson’s strategy is conservative enough to keep one out of trouble, but it may also hold one back. The conventional rule may mislead players by requiring more bankroll than they actually need or by requiring too small a bankroll for what they need. Nevertheless, if your bankroll were to meet all three requirements, this should provide a good deal of psychological comfort.

Your comfort level is the final aspect of bankroll. We want to mention before getting into a more detailed analysis of how to use these bankroll requirements in actual practice. Part of the reason why you want to calculate your bankroll requirement is to know where you stand. If you know that you have a bankroll large enough so that your chances of going broke are only 1 in 100 or 1 in 1000, this provides the peace of mind to allow you to continue playing your A-game even if you lose a few buy-ins in the course of a session. Your own psychological comfort is important, and this is purely subjective. If, however, you understand the three basic rules and what they explain, this should give your subjective intuition some grounding in reality. This is important, particularly, for those who are more conservative and might hinder their development as players and consequently their ability to earn income by being overly cautious.

How To Make Bankroll Plan

• Now, let’s put the foregoing to use in constructing a bankroll plan. How should you proceed? First, you should begin by determining your own salary or wage. If you are playing indefinitely, then you’ll need a yearly amount you want to earn. If you are playing for only a few months, then set a total for those months. For example, you might set a yearly goal of $30K.
• Second, you will need to determine how many hours per day or per week you want to spend playing poker. Let’s say you want to spend 30 hours per week. You will also need to determine how many hours you need to play per day in order to achieve your income goal. You do this by extrapolating from your win rate. So, let’s say your table win rate is $20/hr and you plan to pay yourself $15/hr. At that pay rate you will need to put in 2000 hours over the course of the year, or 38.46 hours per week. Hopefully the two match up or you have a nice surplus, but in our example, you have a shortage. In this case, you’ll need to make some difficult choices. You may need to play more hours or pay yourself more to achieve your income goal, but each of these choices brings costs. Perhaps you would like to spend more of your time away from the tables. You may have to sacrifice these other goals. If you pay yourself more, this will stress your bankroll and/or require a much higher bankroll to move up to the next level.
• This brings us to step number three. Determine bankroll needed on each bankroll requirement model. Do you have 300BBs for limit or 2000bbs for no limit? Can you buy-in for only 5% of your roll? Is your risk of ruin 1% or less with your current bankroll?

Examples Of Bankroll Plan

We strongly recommend using the risk of ruin formula as the dominating requirement here. If it disagrees with the other two, so much the worse for those two. Risk of ruin is far more accurate. If, however, your bankroll meets risk of ruin and the other two, this should only add to your psychological comfort. Finally, write out table win rate, effective win rate, hours you will have to play on a daily basis, and required bankrolls; have a long hard look at those numbers and a long hard look in the mirror when you ask yourself if this is really possible. If you determine that it is, then you are ready to start playing professionally. This is all still a bit abstract, so let’s examine a couple of examples, which will demonstrate the process and the principles involved.

Example 1:

Aspiring youngster seeks to play poker for summer job. Her expenses over the summer will total somewhere around $4000 (or $1250 per month). She has been playing online limit hold’em exclusively and is currently playing 2/4 with a bankroll of $1400. She would like to pay herself $12/hr playing 30 hours a week for 12 weeks. This is a total summer income of $4320, which will cover the bills and leave a very slight amount left over for fun or unexpected expenses.
She currently makes 1BB/hr per table while four-tabling 2/4 limit, which means her total hourly win rate is $16/hr. She also, however, gets the occasional deposit bonus and is planning to start at a new site for the summer to take advantage of the promotional deposit bonus – such as the one for Full Tilt Poker over the menu here at Pokerbroz. Now that bonus will probably clear at about $2.70/hr per table ($10.80/hr for four tables), so in addition to the table win rate, she will also get the bonus, which will give her a total gross win rate of $26.80/hr. Small wrinkle, however, she will clear that bonus in roughly 56 hours, so she will only make this rate for the better part of two weeks. Since what we want to discover first off is the initial bankroll requirement, we can go ahead and work with the current win rate numbers. Assuming that we have enough bankroll, we can then figure the third month separately. Now, she wants to pay herself $12/hr, so her effective win rate is $14.80/hr, which she will keep in the bankroll; hence growing the bankroll. Her standard deviation is $80/hr.
Let’s check the various requirements. Does she have 300BBs? Check. The Ferguson requirement is geared for no limit play, so we can ignore that one. Does she have risk of ruin of 1% or less? Glance back at the first part of the article for an explanation of this concept and the formula (if you need to):
1% Bankroll = -(80squared/2×14.80)ln(1%)
1% Bankroll = -(6400/29.60)(-4.605)
1% Bankroll = $995.68
So, another check. As she wins, this will get better, but she only has 56 hours of play before the bonus runs out. Will she have enough with the reduced win rate? Without the bonus, her effective win rate will only be $4/hr. She will then need a bankroll of $3684. She will be adding $14.80/hr to her bankroll for the first 56 hours, which will put in $828.80, but that is not enough to get to $3684 starting from only $1400. A 5% risk of ruin requires $2396.80, which still leaves her short. Conclusion, this would be very risky as a summer job. The likelihood that she will bust her bankroll is greater than 5%, or in other words, she will go bust more than one time in twenty. Couple that with the added knowledge that this is a risky gambit and a bad run of cards is likely to be psychologically devastating. She cannot solve this problem by playing more hours either. She could drop down to 1/2, but then assuming a similar win rate, she would not earn enough to cover the $12/hr she needs for expenses. Thus, this is simply not a workable plan.
One approach to solving this problem would be to move to a new site and take advantage of another deposit bonus, since this worked so well initially. Let’s say that after the 56 hours at Full Tilt Poker, she signs up at Bodog for the 10% deposit bonus, which is an instant bonus. Isn’t that nice? So if she takes her $2200 bankroll out and moves it to the new site, she will get $220 bonus instantly, which will inflate her bankroll to more than $2400, but this will still not be enough. She needs $3684. If instead, she withdraws this amount after clearing the bonus, she could count it as income added to her hourly rate.
Bodog has a three table max rather than the four max at Full Tilt, so her table win rate will drop to $12/hr. She can expect somewhere around $6/hr per table, however, from the bonus. This would make the total gross hourly rate $30/hr. Since she will be taking out $12/hr, her effective rate is $18/hr, but only for about 12 hours. Then she will face the same problem of lack of bankroll as before. Note that she will clear this bonus in less than a week, and will have to move quickly to another site.
Basically, she will need to continually move funds to new sites throughout the summer. If she plans ahead she may be able to set a schedule for what sites to play to pad the win rate with various bonuses. If this is possible, she can probably pull this off for the summer, but she would spend some extra time transferring funds around. I would think this would be somewhat stressful if one did this indefinitely. That stress doesn’t prevent the existence of various “bonus whores” from populating the majority of online card rooms, but it seems like a difficult life.
Now, things change dramatically if she has an alternate source of income and can play poker on the side. If she gets a job that covers half of what she needs, i.e., she only needs to pay herself $6/hr from poker, then watch what happens. Her effective win rate post bonus is $10/hr, which gives us a bankroll requirement of only $1473.60. She’s starting with $1400 and so will easily cover $73.60 in the first 56 hours of play. She can still play different card rooms over the summer to take advantage of bonuses, but there will be no pressure to scout out the next bonus. Note also the rather large difference here between the bankroll one needs relative to effective win rate.
Playing poker as a part-time source of income takes enormous pressure off your bankroll. This is one significant bankroll advantage that the semi-pro has over the full-time professional. Moving full-time to poker is a risky step and must be taken with extreme caution as the bankroll is not replaceable and going bust means the end of your poker career and the end of your income.

Example 2

Let’s consider a second example in which a long-term professional player faces a couple important decisions. The first is how to deal with significant downswings that reduce one’s bankroll. The second is growing one’s game and moving up to a higher blind level. We’ll assume that our pro has been playing for two years but has played several years prior as an amateur and semi-professional, and so has significant data on numerous levels of play. He is currently playing four tables simultaneously at a $1/$2 blind structure in no-limit hold’em and winning $40/hr total. His standard deviation is about $180/hr. His bankroll is only $4200, as he had an unexpected car expense.
Let’s begin with whether the current bankroll is adequate to his current blind level. $4200 is more than 2000bb’s so it meets the conventional wisdom standard. He can buy-in at most sites for the max (100bb’s or $200) and still be under Ferguson’s 5% requirement. Now to compute the risk of ruin, we need to know not just the table win rate but also the effective win rate. Let’s say that he is paying himself $20/hr and so his effective win rate is $20/hr. With his effective win rate and standard deviation numbers he needs a bankroll of $3730, which he has. Thus, his current bankroll meets all three standards.
What happens if he plays a couple sessions and loses three or four buy-ins? Let’s say he loses $500, dropping his bankroll to $3700. What should he do now? He is only just below the 1% risk of ruin number, so this is not yet reason to panic. Let’s say, however, that he hits another bad run of cards in the next session and loses another $400, dropping his bankroll to $3300. There are two numbers that he should keep in mind when deciding whether to drop down a level to protect his bankroll. The first is the 1% risk of ruin at the lower blind structure. In the past he won $25/hr at those stakes, and had a standard deviation of $90/hr. Now at $25/hr he will only have an effective win rate of $5/hr. Note that this is a compelling reason to stay at the current stakes, since the 1% risk of ruin number given these assumptions at a 50c/$1bb game is $3730. Uh oh, he is already well below that number, and note that it is the same as the number he needs at the current stakes.
Moving down in stakes will not help unless he can pay himself less of his winnings. This leads us to the second number, which is the revised effective win rate. Let’s say that he can drop his pay to $15/hr and still cover the absolute necessities. Life will not be fun during this period, but it may be necessary. This will increase his effective win rate to $10/hr at the lower stakes, which yields a 1% risk of ruin figure of $1865. If he is willing, and he really better be, to tighten the belt right now at the current stakes, his new 1% risk of ruin bankroll is $2984. These new numbers should give the pro some peace of mind. He is in front of the revised bankroll number and well in front of what he would need if he were to pass it and drop to the lower blind level. He should be able to play his normal game without fearing busting his bankroll or getting trapped.

It is very easy for pros to get trapped and bust, if they do not make the necessary changes in time. Let’s say that our pro didn’t figure his risk of ruin and just kept playing the current stakes and paying himself the same rate, but kept running badly dropping his bankroll to $2000. At that point, he is well below even the 5% risk of ruin number, teetering right on the brink of disaster. Perhaps now he drops to the lower stakes, as conventional wisdom (2000bbs) would suggest, but with such a reduced effective win rate he cannot reduce the risk to his bankroll, even at these lower stakes. In fact, $2000 is below the 5% risk of ruin ($2427) at these lower stakes, coming in at around 8%, which is very dangerous (about the chance that someone’s smaller pocket pair is going to catch a set and crack your aces when you get all-in on the flop). The pro cannot drop another level, as this would leave him unable to pay the bills, and so the pro is trapped on a sinking ship. Sometimes things work out; sometimes the aces get cracked.

This example is instructive as it indicates that one needs to figure several numbers to get a picture of what life will be like if a bankroll is threatened. You need to know your current 1% risk of ruin number for both the current level and the level below. It may be that dropping a level will not help or only help slightly. You also need to know how much of a pay cut you can withstand if things go bad so that you can also figure the revised risk of ruin numbers. This is often far more effective at preserving your bankroll’s health than dropping stakes. Finally, as a matter of psychological comfort, you should protect your bankroll and leave some margin for error, so that you do not spend mental energy worrying about your fate as a poker player, particularly as you look down at a pair of aces wondering whether they will get cracked and cost you a stack that you need to cover the electric bill for the month.

Let’s turn our attention to happier thoughts: moving up a level. When one considers whether to move up a level, things tend to be going well, but the bankroll also needs to be able to withstand such moves. Let’s say that our pro tightens his belt and recovers his losses and progresses on up the bankroll ladder. At what point should he consider playing in the bigger game? Conventional wisdom would suggest that he wait until he has collected 2000bbs; i.e., he would need $8000 before moving up. What does the risk of ruin formula require? If he has never played at this level, he will need to estimate his win rate.

Generally speaking, one’s win rate will diminish as one moves up in levels. Estimating how much to take off is difficult and can only be done by scouting out the next level and determining how much more difficult this level is than the current one. Let’s say that our pro estimates his likely table win rate at $70/hr (it is $40/hr at the current level). His effective win rate would be $50/hr. His standard deviation is a reflection of his style of play and so will remain roughly the same; hence, he can simply double it when moving up to double stakes. Thus, his estimated standard deviation is $360/hr. His 1% risk of ruin number given these figures would be $5968. That number is significantly less than the conventional rule and demonstrates the overly conservative nature of that rule for a player with this particular playing style.

Now, if things go poorly at the next level, the pro needs to drop back to the current level immediately. This is mainly due to the psychological comfort that comes with playing at a level that one has done well at for an extended amount of time. Moving up a level often produces anxiety that affects one’s play and produces inferior results. The professional needs to protect himself or herself from any extended bad play. The professional, then, takes shots at the next level rather than making any permanent move. When things go well, the pro continues to play at the next level. The pro should continue this approach until reaching a 1% risk of ruin figure for the next level.

In our example the pro would need to take shots until his bankroll reaches $6714. At this point, he would have a 1% risk of ruin for the $3/$6 no limit game. Note once again that this figure is far below the conventional rule or the Ferguson rule. In fact, this number is well below what these other approaches require for the $2/$4 game, which further underscores how conservative these approaches can be for players with a low variance game.

The goal of the professional is to make money. The higher the game you can play in, the greater is your ability to earn an income. Playing in a higher game brings greater flexibility to your play. You can play fewer hours and earn more than you did previously. That’s almost universally a good thing. You can also play the same number of hours and earn almost twice what you did before. That’s also almost universally a good thing. Therefore, moving up when you are ready is almost universally a good thing.

One might describe my approach as overly aggressive, but this judgment stems from a comparison with the conventional approach. The statistical approach based on one’s risk of ruin is a sound strategy. It is tailored precisely to one’s own playing style whereas the conventional rule is a one size fits all approach. Working with your risk of ruin can open up your prospects and provide you with the confidence to move up in levels far more quickly than the conventional rule would dictate, and this move up is not aggressive any more than getting your money in as a 99 to 1 favorite is aggressive. If you were to ask any player whether that were a risk worth taking, the answer would be yes. Moreover, as I described in the discussion of moving down levels, your true risk of ruin is much less provided that you are willing to make the necessary adjustments in time.

Poker Bankroll Risk Of Ruin Calculator Formula

Although the conventional rule can be overly conservative, it can also be overly liberal. A loose aggressive player may be misled into moving up sooner than is advisable. For example, if such a player were playing a $1/$2 no limit game and making $64/hr but with an effective win rate of $44/hr and a standard deviation of $400/hr, the 1% risk of ruin bankroll requirements for the $1/$2 game would be $8373. The conventional rule would recommend only $4000. Thus, for the loose aggressive player, the conventional rule can massively understate necessary bankroll. If a loose aggressive player with the numbers I’ve assigned were to play in the $1/$2 game with only a $4000 bankroll the risk of ruin would be greater than 11%. In other words, this player would go bust more than one time in every ten. Whether your play is tight or loose, you should work with the risk of ruin numbers to get a more precise picture of what your bankroll requirements are.

Poker Bankroll Chart

If you are contemplating a move from amateur to semi-professional or professional, then you should begin by setting your income goal and working from there to determine whether you can play the necessary hours and whether you have the necessary bankroll. I have demonstrated the limitations of the conventional rule and the Ferguson rule. In their place, you should develop a more accurate approach tailored to your own style of play and particular results. This will produce an honest assessment of what is required to make the leap from amateur to professional. Similarly, the semi-professional can make a more accurate assessment of what is required to make the jump to full-time play. Finally, all players can more accurately assess their bankroll requirements for their current level, when to move down, and when to move up.